Assalamu'alaikum Wr. Wb
Kali ini kami akan memberikan penjelasan rangkuman dan pembahasan tentang bab Polinomial. Selain agar kami lebih memahami, postingan ini juga akan membantu teman - teman yang akan mempelajari bab Polinomial ini.

A. Pengertian Polinomial
Polinomial adalah suku banyak terhingga yang disusun dari peubah/variable dan konstanta. Operasi yang digunakan hanya penjumlahan, pengurangan, perkalian dan pangkat bilangan bulat tak negatif.
Polinomial adalah suku banyak terhingga yang disusun dari peubah/variable dan konstanta. Operasi yang digunakan hanya penjumlahan, pengurangan, perkalian dan pangkat bilangan bulat tak negatif.
Yang memuat :
a). Bilangan cacah bersusun
b). Koefisien
c). Konstanta
d). Variabel
e). Operasi matematika.
B. Bentuk Umum Polinomial
anxn + an-1xn-1 + an-2xn-2 + a1x .. + a0 = 0
an ≠ 0
Suku banyak ini disebut berderajat n, karena pangkat tertinggi dari variabel suku banyak ini adalah n.
C. Pemjumlahan, Pengurangan dan Perkalian Polinomial
Diketahui suku banyak f(x) dan g(x) sebagai berikut
f(x) = 2x3 - x2 + 5x - 10
g(x) = 3x2 - 2x + 8
Tentukan :
a). f(x) + g(x)
b). f(x) - g(x)
c). f(x) x g(x)
Penyelesaian
a). f(x) + g(x) = (2x3 - x2 + 5x - 10) + (3x2 - 2x + 8)
= 2x3 - x2 + 3x2 + 5x - 2x - 10 + 8
= 2x3 + 2x2 + 3x - 2
b). f(x) + g(x) = (2x3 - x2 + 5x - 10) - (3x2 - 2x + 8)
= 2x3 - x2 - 3x2 + 5x + 2x - 10 - 8
= 2x3 - 4x2 + 7x - 18
c). f(x) x g(x) = (2x3 - x2 + 5x - 10) × (3x2 - 2x + 8)
= 2x3(3x2 - 2x + 8) - x2(3x2 - 2x + 8) + 5x(3x2 - 2x + 8) - 10(3x2 - 2x + 8)
= 2x5 - 4x4 + 16x3 - 3x4 + 2x3 - 8x2 + 15x3 - 10x2 + 40x - 30x2 + 20x - 80
= 2x5 - 7x4 + 33x3 - 48x2 + 60x - 80
D. Pembagian Polinomial
1. Dengan cara bersusun
contoh 1
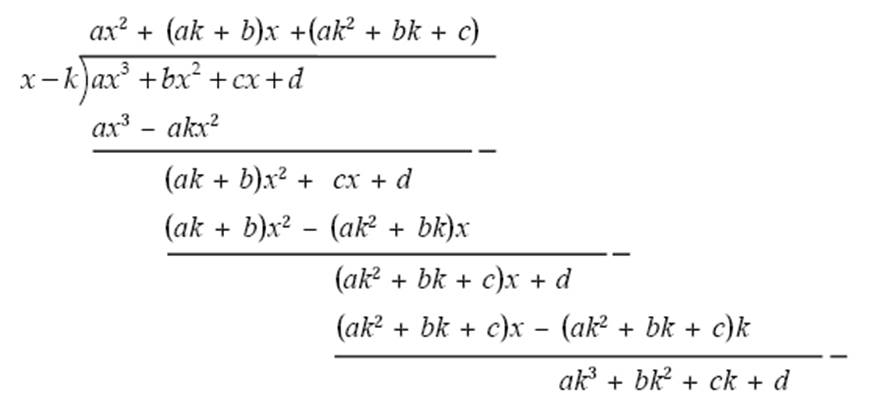
contoh 2
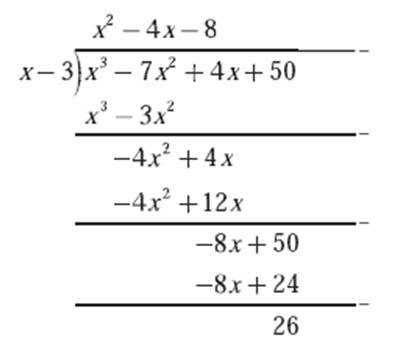
2. Dengan cara horner
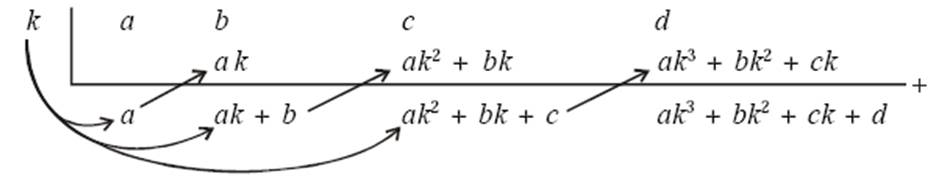
Contoh soal menggunakan cara bersusun dan horner
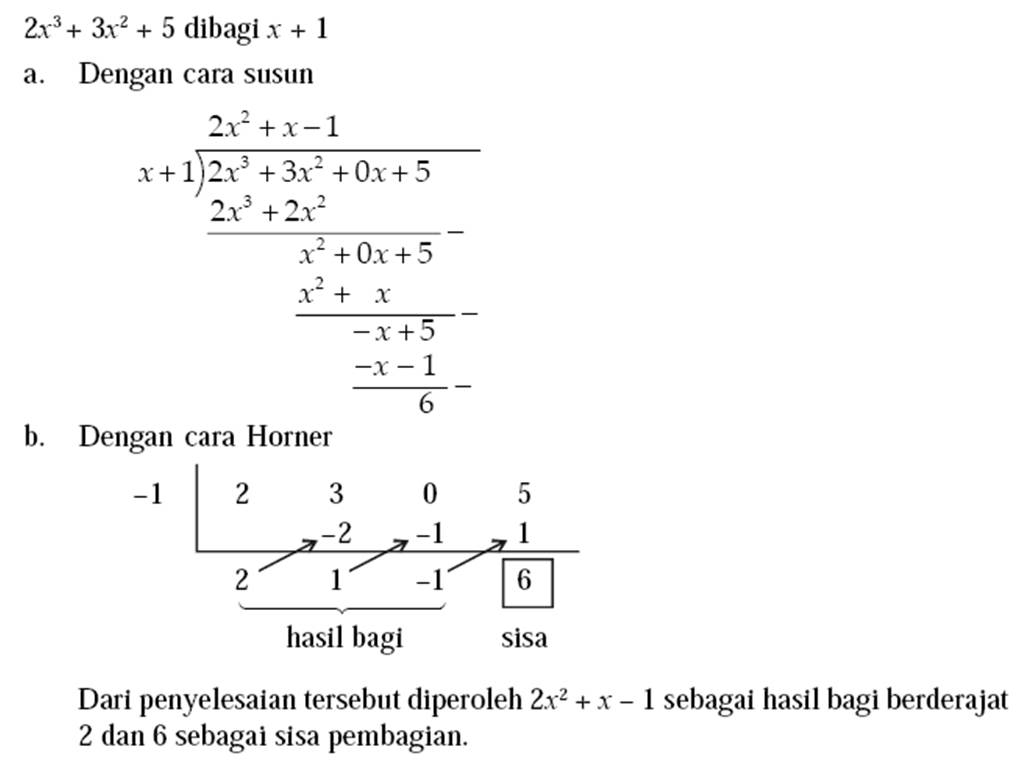
5. Teorema Sisa
Konsep teorema sisa mirip dengan konsep pembagian Sukubanyak. Untuk teorema sisa sendiri ada 3, yaitu teorema sisa untuk pembagi berbentuk (x-h), pembagi berbentuk (ax-b), dan pembagi berbentuk (x-h1)(x-h2). Berikut adalah tiga teorema sisa:
- Teorema 1: Jika sukubanyak P(x) berderajat n dibagi (x-h), maka sisa pembagianya adalah S=P(h).
- Teorema 2: Jika sukubanyak P(x) berderajat n dibagi (ax-b), maka sisa pembagianya adalah
 .
. - Teorema 3: Jika sukubanyak P(x) berderajat n dibagi (x-h1)(x-h2), maka sisa pembagianya adalah

contoh soal :
Suatu suku banyak jika dibagi oleh x + 2 bersisa -13 dan jika dibagi x - 3 sisanya 7. Tentukan sisanya jika suku banyak tersebut dibagi x2 - x - 6
Suatu suku banyak jika dibagi oleh x + 2 bersisa -13 dan jika dibagi x - 3 sisanya 7. Tentukan sisanya jika suku banyak tersebut dibagi x2 - x - 6
cara 1
k(x) = x2 - x - 6
k(x) = (x + 2) (x - 3)
kita tahu bahwa jika dibagi oleh x + 2 bersisa -13 dan jika dibagi x - 3 sisanya 7
Maka, k(-2) = -13 dan k(3) = 7
Jadi kembalikan ke rumus sisa
s(x) = mx + n
s(-2) = -2m + n = -13
s(3) = 3m + n = 7
s(x) = mx + n
s(-2) = -2m + n = -13
s(3) = 3m + n = 7
Lalu Kita menggunakan eliminasi
-2m + n = -13
3m + n = 7
-5m = -20
m = 4
Lalu Substitusikan ke persamaan
12 + n = 7
n = -5
Lalu kembalikan ke rumus s(x) = mx + n
Maka Sisa Polinomial jida dibagi x2 - x - 6 Hasil nya 4x - 5
-2m + n = -13
3m + n = 7
-5m = -20
m = 4
Lalu Substitusikan ke persamaan
12 + n = 7
n = -5
Lalu kembalikan ke rumus s(x) = mx + n
Maka Sisa Polinomial jida dibagi x2 - x - 6 Hasil nya 4x - 5
6. Teorema Faktor
Untuk dapat memahami teorema faktor, kita terlebih dahulu harus memahami teorema sisa (saya jelaskan di subbab sebelumnya). Diberikan sukubanyak berikut ini
P(x) = (x-1)(x2+1) = x3-x2+x-1
Perlu anda ketahui dua hal:
1). (x-1) adalah faktor dari P(x).
2). P(1) = 0 atau sisa = 0.
Dari dua hal diatas, dapat kita simpulkan teorema faktor:
Suatu sukubanyak P(x) memiliki faktor yaitu (x-h) jika dan hanya jika P(h) = 0 atau sisanya = 0.
Pembuktian :
- Kita ketahui dari pembagian sukubanyak bahwa P(x) = Q(x) . H(x) + S(x)
- Dari teorema sisa kita pelajari bahwa P(x) = (x-h).H(x) + S, dengan S = P(h). Kita ketahui bahwa teorema faktor berlaku jika dan hanya jika P(h) atau sisa = 0.
P(x) = (x-h).H(x) + S
Karena P(h) = 0, maka
P(x) = (x-h).H(x)
Ini menunjukkan bahwa (x-h) adalah faktor dari P(x), jika dan hanya jika P(h) = 0
Sekian pembahasan mengenai materi Polinomial (Suku Banyak). Mohon maaf apabila ada kekurangan. Semoga dapat dipahami dengan baik dan dapat bermanfaat bagi kita semua.
Daftar Pustaka
Internet :
Ramli, Dhamara. 2015. "Rangkuman, Soal, Pembahasan Bab Polinomial", https://dhamarar.blogspot.com/2015/09/rangkuman-soal-pembahasan-bab-polinomial.html
Opan, 2012. "Pembagian Polinom", https://maths.id/pembagian-polinom.php
https://lovemathematin.wordpress.com/ringkasan-materi-sukubanyak-polinomial/ (tidak ada keterangan penulis)
Buku :
Sembiring, Suwah. 2013. Matematika Berbasis Pendidikan Karakter Bangsa (KTSP) (untuk SMA/MA Kelas XI IPA). Jakarta: Yrama Widya.
Sukino. 2013. Matematika - Kelompok Peminatan Matematika dan Ilmu Alam untuk SMA/MA Kelas XI Kurikulum 2013. Jakarta: Erlangga.
Noormandiri, B. K. 2016. Matematika Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam untuk SMA/MA kelas XI semester 2.Jakarta: Penerbit ErlanggaPenerbit.
Oleh Kelompok 9 XI MIPA 3
Nama Kelompok :
1. Amelia Dinda Zalwani
2. Qonitha Arifa
3. Rizky Anggoro Putra
4. M. Fathan Mubina (TIDAK KERJA)